QC > Math > chanusa > 634 > Homework Syllabus • Topics • Schedule • Homework • 634
Homework Assignments
Graph Theory – Fall 2008
NOTE! Refresh your browser to get updates!
Homework 17
Special Practice Homework (Not to be turned in)
  • Exam 2: Thursday, December 18, 2008 from 6:15 to 8:15
  • Extra Office Hours: Tuesday, December 16 and Thursday, December 18 from 4:30 to 6:20 (6:05 on Thurs).
    I will also be in my office some on Wednesday so if you would like to stop by, email me and we'll work out a time.
    Questions by email are also welcomed.
  • Exam 2 covers planarity and algorithms. (See topics.) Here are some practice problems.
    • 7.1.1, 7.2.3, 9.1.7, 9.1.8, 9.1.9, 9.1.10
    • 17-1.  Find an ``Euler's formula'' for disconnected graphs.
    • 17-2.  For each of the graphs in your table of statistics, find its crossing number, thickness, and genus.
    • 17-3.  Practice network flow on this network.
    • 17-4.  In Problem 15-4, give two different schedules that show that this amount of commodity can be shipped from A to D in five days or show that there can not possibly be two different shipping schedules.
    • 17-5.  With four men and four women, find sets of preferences for the men and women such that running the Gale-Shapley algorithm with the men proposing and then with the women proposing gives two different sets of marriages. Show that your answers illustrate the optimality/pessimality of the algorithm.
    • 17-6.  (hard!) It is possible to use max flow/min cut to determine a vertex cover in a bipartite graph. (A vertex cover is a set of vertices that is adjacent to every edge in the graph.) Given a bipartite graph G with bipartition V=X union Y, set up a network like we did in class: create a super-source s that is adjacent to all vertices in X; then create a super-sink t that is adjacent from all vertices in Y. Next, assign capacities to all edges: for the edges you added, give them capacity 1; for the edges of the original graph, give them capacity infinity. Now run the Ford-Fulkerson algorithm on this graph to determine a max flow x* and min cut S*. The set of vertices S* contains some vertices V of X and some vertices W of Y. Prove that the set [(X\V) union W] is a vertex cover of G. [Note: you will need to show that every edge in G is adjacent to some vertex in this set.]
    • Here is a past exam: here. Again, there will be questions you can not answer since different material was covered.
  • You should also go over your past homework problems.
  • Bonus point opportunity: You may receive five homework bonus points if you complete the following assignment.
    • I would like you to write a letter to the students entering in the next graph theory class I teach. This will be a letter which explains to them what they should expect from the coming semester in graph theory. You should explain what ``graph theory'' is in your own words, and add some sort of anecdote about something you learned in class this semester. I'm sure you have had the opportunity to explain to your friends or family what you learn in this class, and this will give you a chance to organize those thoughts. The letters should be at least a half-page long; I plan to read two or three letters to incoming students the next time I teach the class. I appreciate the time you will put into such a request, so thank you in advance.
Homework 16
To be prepared for discussions on Thursday, December 11, 2008
  • Please fill out the online course evaluation. This will help me improve my teaching. I especially appreciate thoughtful comments left in the short answer part of the survey. The deadline for submitting your evaluation online is December 11th. I will not have access to your comments until January, long after your grades are submitted, so feel free to be honest.
  • Read Section 7.2. Then complete the following problems.
    • 16-1.  Use the Hungarian algorithm to solve problem 7.2.2. Use the initial matching a,4; c,6; e,2; h,5.
    • 16-2.  7.2.1
    • 16-3.  Show that the Hungarian Algorithm does not work for non-bipartite graphs.
    • 16-4.  Prove that the Gale-Shapley algorithm is female-pessimal when run with the men proposing.
    • 16-5.  Run the Gale-Shapley algorithm with the following sets of preferences with the women proposing:
      Women's Preferences
      AprilBettieCarolDelphiEve
      1st ChoiceFFGGH
      2nd ChoiceGHIHF
      3rd ChoiceIIFJI
      4th ChoiceJGHIG
      5th ChoiceHJJFJ
       
      Men's Preferences
      FreddieGregHaroldIsaacJoe
      1st ChoiceCEAEB
      2nd ChoiceBBDCD
      3rd ChoiceECBAA
      4th ChoiceAAEBC
      5th ChoiceDDCDE
Final Project
To be turned in on Tuesday, December 9, 2008
  • Submit the final version of your project through Blackboard; this link might send you there.
Homework 15
To be turned in on Tuesday, December 2, 2008
  • Read the max flow / min cut handout from class and Section 7.1. Then answer the following questions:
    • 15-1.  Exercise 29.2, Parts i and ii, from the handout in class
    • 15-2.  Find the max flow and min cut in this network: (PDF)
    • 15-3.  The market for kumquats is booming!
      Five markets (I through V) each have put orders into the five large kumquat distributors (A through E).
      A has 5 kumquats and can deliver to I, II, and III.
      B has 4 kumquats and can deliver to I, III, and IV.
      C has 2 kumquats and can deliver to II and III.
      D has 5 kumquats and can deliver to III and V.
      E has 4 kumquats and can deliver to IV and V.
      Market I desires 5 kumquats, II desires 2, III desires 4, IV desires 6, and V desires 3.
           Is it possible for all the markets to receive their desired quantity of kumquats for the distributors? If so, give a valid transshipment. If not, explain why not.
    • 15-4.  On the dynamic version of a network from class, use the method of max flow / min cut to determine the maximum amount of the commodity that can be shipped from Warehouse A to Warehouse D in five days. [Assume there is infinite storage of a commodity at every warehouse.] What is the schedule of shipments that transports this maximum amount of commodity from A to D?
    • 15-5.  A spanning tree T in a connected graph G is a subgraph of G that is a tree and includes every vertex of G. (See also p.20 and Section 7.1 in the book.) Prove the correctness of the following algorithm to find a spanning tree of a graph. [Prove that the algorithm terminates and that the output of the algorithm is a spanning tree of G.]
      Input: A graph G with n vertices.
      Preprocess: Label the vertices 1 through n, color them all white. Let T be a set of edges, initially empty.
      Repeat: For the lowest numbered white vertex v, order the edges incident with v. Going through each edge e from first to last, determine if including e in T would create a cycle in T. If it would not create a cycle, place e into T (T is growing.) If it would create a cycle, do not add e to T; go on to the next edge. Once every incident edge to v has been checked, color v black. If all vertices are black, go on to the next step. Otherwise, repeat this step.
      Output: Output the graph T, a spanning tree of G.
  • Your finalized project is due Tuesday, December 11 9; presentation homework #16 will be due Thursday, December 13 11.
No homework is due Tuesday, November 25, 2008.
Instead, make sure to bring in two paper copies of your final draft of your project.
Homework 13
To be prepared for discussions on Tuesday, November 18, 2008
  • Read Sections 9.1, 9.2 (to p193), and 10.3 (to p230). You may also find this site useful. Then answer the following questions:
    • 13-1.  (a) 8.2.3 and (b) 8.2.4
    • 13-2.  Try to prove the Four Color Theorem by emulating the argument from class using Kempe Chains. What goes wrong?
    • 13-3.  Show that the Petersen graph is a minor of the graph from Homework Question 8-3.
    • 13-4.  (a) 9.2.2 [Do not use the formula from the book.] (b) 9.2.4
    • 13-5.  (a) Find an embedding of K6 on the torus.
      (b) Show that the generalization of Euler's formula holds in this case. (That p-q+r=2-2g.)
    • 13-6.  Statistics of non-planarity on the Petersen graph P: (a) 9.1.6 (b) Find the thickness of P. (c) Find the genus of P.
Homework 12 Final Version
To be turned in on Tuesday, November 11, 2008
  • Read Sections 8.1, 8.2, 8.3, and 9.1, along with the planarity definitions handed out in class. Then answer the following questions:
    • 12-1.  Use an argument involving girth to prove that the Petersen graph is not planar.
    • 12-2.  This question has to do with planar duality:
      (a) Show that the wheel Wn is self-dual.
      (b) Show that the planar dual of the octohedron is the cube and vice versa.
      Find a graph that has two non-isomorphic planar duals. [Hint: Look for different planar embeddings.]
    • 12-3.  8.1.9abc
    • 12-4.  Prove that the graph G in Figure 9.1.18 is non-planar using two methods:
      (a) Find a subdivision of K3,3 or K5 that is a subgraph of G.
      (b) Through a series of edge deletions and edge contractions, show that either K3,3 or K5 is a minor of G
    • 12-5.  9.1.1ab
    • 12-6. (Bonus)  Play the planarity game. Complete levels 1-4 for two bonus points and complete levels 1-7 for two more (four total). Write down the level you complete and your score on your homework.
Homework 9
Special Practice Homework (Not to be turned in)
  • Midterm: Tuesday, October 28, 2008
  • Extra Office Hours: Thursday, October 23 and Tuesday, October 28 from 4:30 to 6:20.
  • I ask that you post a question (and/or a response) on the discussion board for Thursday's class. [Not required, but suggested.]
  • The midterm covers Sections 1.1-1.3, 2.1-2.3, 3.1, and connectivity, knight tours, and de Bruijn sequences. (See topics.)
  • In preparation for the midterm, I have compiled some practice problems.
    • 2.1.4, 2.1.6, 2.4.23, 3.1.11, 3.2.8
    • 9-1.  (a) Prove that there is no closed knight's tour on the 3x8 grid without citing the theorem from class. (b) Find a closed knight's tour for the 5x6 grid.
    • 9-2.  Prove that at a party with 49 people, there is always a person who knows an even number of others. [Assume acquaintence is mutual.]
    • 9-3.  Determine the girth and the diameter of the following graphs: Kn, Km,n, Petersen, Dodecahedron, 5D-cube
    • 9-4.  Prove or disprove the line graph of an Eulerian graph is (a) Eulerian and (b) Hamiltonian.
    • 9-5.  Prove or disprove: the line graph of a Hamiltonian graph is Hamiltonian.
    • 9-6.  Explore Theorem 2.3.2---draw out K10 and find the 4 Hamiltonian cycles and 1 1-factor that are guaranteed by the theorem.
    • 9-7.  Draw the binary de Bruijn graph of order n=5. Find one binary de Bruijn sequence of order 5. (Note: This will be a sequence of length 32.)
    • 9-8.  Show that the Petersen graph P is 3-connected, and determine its edge connectivity.
  • You should also go over your past homework problems.
  • You may have fun practicing trying to complete a closed knight's tour
  • You may enjoy this website: http://www.ktn.freeuk.com/index.htm
  • I am also including two past exams, here and here. MAJOR CAVEAT: The students taking these exams had an hour and a half (you have an hour and a quarter), and they covered different material from you, so there are questions you will not be able to solve. I am providing these exams so that you get a flavor for my style of exam giving, and NOT as indicative of the questions you should expect on the exam.
Homework 8 Final Version
To be turned in on Thursday, October 16, 2008
  • Read Section 2.3.
    • 8-1.  (a) Prove or disprove: If H is a subgraph of G, then κ(H)≤κ(G) (b) Prove or disprove: If H is a subgraph of G, then χ'(H)≤χ'(G).
    • 8-2.  Is Figure 2.1.5 critical? Justify. (Don't believe everything you read!)
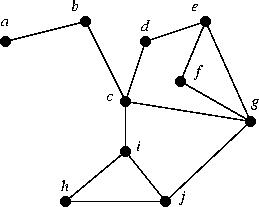
    • 8-3.  Determine and prove the edge chromatic number for this graph:
    • 8-4.  (a) Prove that there is no Hamiltonian cycle in Figure 2.3.4. (b) Find a Hamiltonian path in Figure 2.3.5. (p.40)
    • 8-5.  Determine how many different Hamiltonian cycles there are in (a) Kn. (b) Wn.
Homework 7 (There is no Homework 6)
To be prepared for discussion on Tuesday, October 7, 2008
  • [By 5pm Tuesday] Go online to blackboard and post a question about the past week on the discussion board, in the thread labeled Homework 7. You may also post a reply to another student's post.
  • Read Sections 2.1 and 2.2. Then complete the following problems.
    • 7-1.  Two problems related to the difference between al and um: (a) Suppose that P and Q are two paths of maximal length in a connected graph G. Show that P and Q may not share a common vertex. [Compare this with Question 5-2.] (b) Find an example of a minimal disconnecting set that is not a minimum disconnecting set.
    • 7-2.  (a) Prove or disprove: Every 3-connected graph has no bridge. (b) Prove or disprove: Every 3-edge-connected graph has no cut vertex.
    • 7-3.  2.1.21
    • 7-4.  Determine χ(Wn). For which n is Wn critical?
    • 7-5.  Determine the chromatic number and edge chromatic number of the graph G in the following figure.
    • 7-6.  Find the line graph L(G) of the graph G in Exercise 7-5. Determine the chromatic number of L(G).
Homework 5
To be turned in on Tuesday, September 23, 2008
  • Complete the following problems.
    • 5-1.  (a) 1.3.2 [Prove you are correct.] (b) Exploration Question: Let G have n vertices and n edges. If G has more than one connected component, what can we say about the number of cycles in the graph? Can you determine a formula?
    • 5-2.  1.3.4 (Remember to justify your claim!)
    • 5-3.  Suppose that P and Q are two paths of maximum length in a connected graph G. Prove that P and Q share a common vertex.
    • 5-4.  Show that the wheel graph Wn is 3-connected for all n≥4.
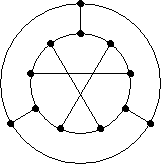
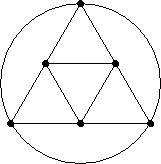
    • 5-5.  Find a maximum minimum disconnecting set and a maximum minimum separating set for each of the following graphs. (Remember to justify!) What is the connectivity and edge connectivity for each graph?
Homework 4
To be prepared for discussion on Tuesday, September 16, 2008
  • [By 5pm Tuesday] Go online to blackboard and post a question about the past week on the discussion board, in the thread labeled Homework 4. You may also post a reply to another student's post.
  • Read Section 1.3. Then complete the following problems.
    • 4-1.  Draw the Schlegel diagram for two of the following polyhedra: Icosidodecahedron, Truncated Icosahedron, Rhombicuboctahedron, Snub Cube.
    • 4-2.  (a) If G is a k-regular graph, what can you say about Gc? (b) If G is a connected graph, what can you say about Gc
    • 4-3.  Give two examples of self-complementary graphs with more than 4 vertices. (n≥5)
    • 4-4. (a) 1.3.1 [Note: T can be any tree satisfying the given condition.] (b) 1.3.12
    • 4-5. We know that in a tree with n vertices, the number of edges is n-1. Prove or disprove: Any graph with n vertices that has fewer than n-1 edges is a forest.
    • 4-6.  Sudoku is sooo 2007! Solve this Hashi puzzle.
      Instructions: Edges connecting the circles (vertices) must be either vertical or horizontal. Up to two edges may be drawn connecting the same circles. The edges drawn may not cross, and the degree of each vertex is the enclosed number. Also, the entire graph must be connected!
             For many more Hashi puzzles and other fun games, visit Hashi puzzles or Puzzle Bridges
Homework 3
To be turned in on Tuesday, September 9, 2008
  • Read Section 1.2. Then complete the following problems.
    • 3-1.  1.1.7
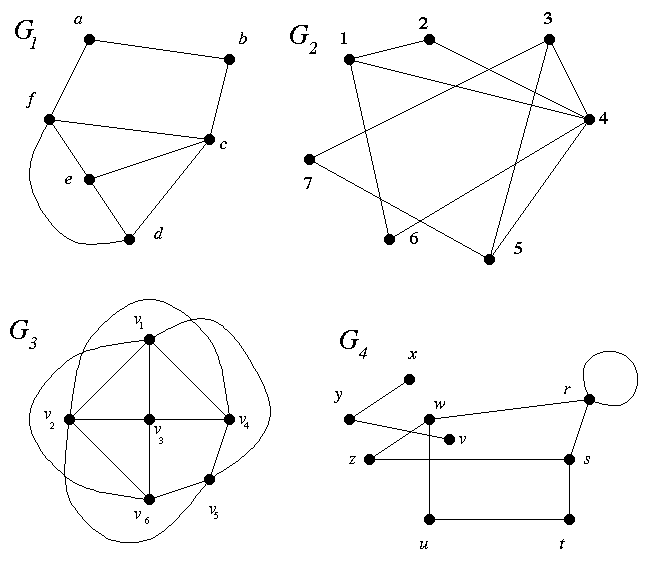
    • 3-2.  Explore the proof of Theorem 1.1.2: The graph below has degree sequence (S1) 4 4 3 3 3 2 2 2 2 1.
      Define (S2) to be 3 2 2 2 2 2 2 2 1. Walk through the steps of the proof of Theorem 1.1.2 in the following way.
      • Let us choose vertex c from the graph to be vertex S from the proof. Determine which of the remaining vertices (a – j) are the vertices Ti and Di from the proof.
      • If you delete vertex S, does the new graph have degree sequence (S2)?
      • Use the method in the proof to modify the graph to be such that removing S gives a graph with degree sequence (S2).
    • 3-3.  (a) 1.2.4 (b) 1.2.5 (Remember to justify that your answers are true!)
    • 3-4.  Explain in your own words the difference equality and isomorphism of labeled graphs. That is, given two labeled graphs, they may be equal and/or they may be isormorphic. Write a couple of paragraphs explaining how these are similar and how they are different, and what is involved in verifying each claim.
    • 3-5.  1.2.10 (The conclusion of your argument should be that three graphs are isomorphic to each other.)
  • Please reference the people you worked with on your homework. (Acknowledgments are nice for everyone!)
Homework 2 (The 2 means WEEK 2)
To be turned in on Tuesday, September 2, 2008
  • Thoroughly read the class web page including the syllabus and schedule. This should answer all the questions that you may have about the class.
  • Go to the class Discussion Board. Introduce yourself on the "Class Introductions" thread. (You need not ask a question on the discussion board this week.)
  • Read Section 1.1. Then complete the following problems.
    • 2-1.  Write a paragraph or two giving an example of where you have seen graphs in real life. (Do not use the examples from class unless you have a unique perspective.) Explain what in your example corresponds to the abstract concepts of vertices, edges, and vertex degree.
    • 2-2.  1.1.1
    • 2-3.  1.1.2ab, both without using Theorem 1.1.2. If you determine that the sequence is graphic, draw a representative graph with the given degree sequence.
    • 2-4.  1.1.4
    • 2-5.  1.1.5
  • Remember what is expected:
    • When the problem says "Find a graph with property A", you need to draw the graph and explain why the graph has the property you claim it does.
    • When the problem says "Prove X" or "Show X", you need to give a rigorous mathematical argument explaining why "X" is true.
    • It may be the case that an example or a counterexample of a graph is the key to your rigorous mathematical proof. If this is the case, you will need to explain why you have drawn it and what purpose it serves.
    • Write in full sentences.
    • Follow the guidelines for turning in homework.

Back to the Graph Theory Home Page.
Christopher Hanusa – Queens College – Mathematics Department.