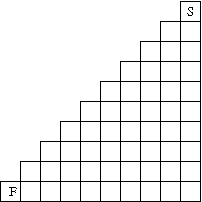• Feel free to try out these problems to help study for the exam.
  • 15S1.  Use the hook length formula to prove that there are the same number of standard Young tableaux of shape λ and λ-conjugate
  • 15S2.  A peak in a Dyck path is a NE step followed by a SE step. (Imagine the peak of a mountain.) Find a bijection between Dyck paths of length 2n with red and blue peaks (every peak can be colored in either of the two colors) and Schröder paths of length 2n. [As always, drawing a picture will help you get started.]
  • 15S3.  Determine the generating function for the sequence e_n defined by e₀=1, e₁=1, e₂=4, and e_n=3c_n-1+1, where c_n is the n^th Catalan number.

• Complete the following four problems, each worth five points!
  • 15A1.  Consider an integer sequence d_n which has as its generating function d(x)=Σ_n≥0 d_nxⁿ=1 - 5 sqrt(1-4x). Determine a formula for d_n in terms of the nth Catalan number, c_n.
    [You should use a generating function argument like we did in class to conclude that s₁=1 and s_n=R_n-1/2 for n≥2.
  • 15A2.  Let g(x) be a generating function for a sequence g_n. If g(x) satisfies ^dg/_dx=(g(x)-1)/(x²-4), determine a second order recurrence that g_n satisfies for n≥2.]
  • 15A3.  Investigate and conjecture a formula for the number of standard Young tableaux of shape λ: 2n=n+n there are for all positive n. For example, when n=3, two valid tableaux are

    1 2 4 3 5 6

    and

    1 3 5 2 4 6

    .

    Prove your conjecture by finding a bijection with a combinatorial interpretation we have seen previously. [Hint: you will likely use the fact that a standard Young tableau of shape n,n is completely defined by its first row.]
  • 15A4.  Determine a formula in terms of s_n and/or S_n for the number of symmetric Schröder paths there are from (0,0) to (2n,0) with the restriction that the path must pass through (n,0). Here, symmetric implies that when we rotate the path about the line x=n, the result looks the same as the initial path.
• Fill out the SOOT evaluation form online on Blackboard. (I think this is the link on Blackboard's homepage.)

Additional Resources:

• (Due by bedtime Wed) Reading report on the reading from 11/19 and the following parts of Section 8.5:
  • from the middle of page 307 through the first proof on page 308.
  • from the bottom of page 309 through the end the section
  • You need not understand the part about the algorithm for "constructing bracketings".
• Read the first page of this file about Young tableaux.
• Complete the following problems.
  • 14B1.  Draw all 10 standard Young tableaux corresponding to n=4.
  • 14B2.  Use the hook length formula to determine the number of standard Young tableaux of shape 321. Then draw them all.
  • 14B3.  (a) 8.30 (b) 8.31
  • 14B4.  Draw all the Schröder paths from (0,0) to (3,3). (Definition on page 309.)
  • 14B5.  Consider the Schröder paths from (0,0) to (4,4) that do not land on the line y=x before arriving at (4,4). How many are there? Conjecture and prove a formula for the number of Schröder paths from (0,0) to (n,n) that do not land on the line y=x.
  • 14B6.  Draw all 11 dissections of a pentagon and determine the corresponding 11 bracketings.

• Read Sections 1-3 (through Thm 4) (pages 4-12) of this file, a series of lectures on partitions by Herbert Wilf.
• Complete the following problems.
  • 13A1.  8.6.27
  • 13A2.  Give a bijective proof of Lemma 1 from Wilf's file, that the number of partitions of n with no parts equal to 1 is p(n) - p(n-1).
  • 13A3.  Determine the generating function for the number of partitions of n satisfying
    (a) there are at most two parts of the same size. (4111 is not allowed since 1 appears thrice.)
    (b) the parts are all of size equal to a power of two. (Example: 844221.)
  • 13A4.  Prove that the number of partitions of n into no more than k parts is the same as the number of partitions of n+k into exactly k parts. (Thanks Wikipedia.)
  • 13A5.  Show that the number of Ferrers diagrams that fit inside an m by n rectangle is (^m+n_m). (Hint: look for a bijection with walks in a lattice.)
• If you did not turn in your outline on Friday, turn it in today! (If truly necessary, turn it in after break.)

• (Due by bedtime Wed) Reading report on the parts of 8.2 you had to read for Monday and Section 8.3 up to the bottom of page 297.
• Complete the following problems.
  • 12B1.  Draw the Ferrers diagram for all partitions of 6.
  • 12B2.  Complete Problem 8.6.26, making sure to draw the relevant Ferrers diagrams and their conjugates.
  • 12B3.  Determine and prove a closed form for {^p₃}
  • 12B4.  Draw all the Schröder paths from (0,0) to (3,3). (Definition on page 309.)
  • 12B5.  In chess, a knight can make moves of type "1 horizontal step and 2 vertical steps" or "2 horizontal steps and 1 horizontal step". Consider the following strange chessboard: 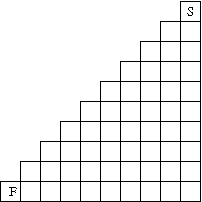If your knight starts in the upper right corner and can only move SSW or WSW, determine how many paths exist in order for the knight to arrive at the bottom left corner?
  • 12B6.  In the spirit of 12B5, conjecture and prove a formula for how many knight paths there are if the size of the triangular board is 3n+1 by 3n+1 instead of 10 by 10.
• Remember: Your project outlines are due Friday November 16. (Or at the very latest by Monday the 19th.) You should explain some preliminary results about your investigations, and discuss the structure of your poster. (Determine how much of the poster will be allotted to what topics.)

• Read Chapter 8.2 from the bottom of page 287 to the middle of page 293 (through Equation (8.21).) (We introduced these Stirling numbers S(p,k)=S^*(p,k)={^p_k} combinatorially and ignored the first half of the chapter.)
• Complete the following problems.
  • 12A1.  8.6.1 (either prove by bijection or equivalence of recurrence)
  • 12A2.  8.6.12 (use our combinatorial interpretation)
  • 12A3.  8.6.15
  • 12A4.  (a) 8.6.11 (b) 8.6.16
  • 12A5.  (*) Let's determine the number of bilateral paths from (0,0) to (0,2n) following NE steps (+1,+1) and SE steps (+1,-1). These are like Dyck paths, but with no restriction about staying above the x-axis.
    (a) Let's determine the generating function b(x) that these paths satisfy. First, notice that every non-trivial bilateral path either starts with an up step or with a down step. If it starts with an up step, then at some point it must return to the x-axis for the first time. Up until this return, the path is following a Dyck path, staying at or above the line y=1. The path then continues as a bilateral path after that point. Starting with this argument, justify that b(x)=1+2x c(x) b(x), where c(x) is the generating function for Dyck paths (the Catalan numbers).
    (b) From this information, deduce that b(x)=1/sqrt(1-4x).
    (c) From this generating formula, prove a formula for the number of bilateral paths from (0,0) to (0,2n). To verify your answer, turn your picture on its side to see that you are counting lattice paths in a square lattice from (0,0) to (n,n).

• (Due by bedtime Wed) Reading report on sections 7.6 and 8.1. In Section 8.1, you do not have to read from the bottom of page 271 to halfway down page 275. Please make sure to hit upon each of the main topics in each section.
• Also read this pdf file, section 1 (and more if it interests you): Catalan interpretations and bijections.
• Complete the following problems.
  • 11B1.  8.6.3
  • 11B2.  In a similar vein to 8.6.3, corresponding to each of the five multiplication schemes and triangulations, determine
    (a) the walks in the lattice from (0,0) to (n,n) above y=x and
    (b) {+1,-1} sequences of length 2n where no partial sum is negative.
  • 11B3.  Use a bijection to show that sequences 1 ≤ a₁ ≤ a₂ ≤ ... ≤ a_n of length n, where each a_i ≤ i are also counted by the Catalan numbers. For example, when n=3, the five sequences are 111, 112, 113, 122, and 123. (Hint: Draw the lattice paths and count the area to the left of the curve.) (From Stanley's Enumerative Combinatorics II)
  • 11B4.  (a) Determine all partitions of the set S={1, :), apple, #, *} into 3 indistinguishable boxes. (b) Determine all partitions of S.
  • 11B5.  Determine all partitions of 7.

• In section 7.5, you do not have to read between the top of page 246 up to Thm 7.5.1. (Do read Thm 7.5.1.)
• 10S1.  5.8.16 and 5.8.18
• 10S2.  Prove that the sum from j=2 to infinity of [1 over (^j₂)] equals 2.
  [Hint: Write the denominator as a polynomial of j, then use partial fractions]
• 10S3.  6.7.20
• 10S4.  6.7.43
• 10S5.  7.8.34
• 10S6.  We can make a four-sided die using a tetrahedron. If the sides of the die are 1, 2, 3, and 4, then there is a particular distribution of possible sums between 2 and 8. Determine a relabeling of the two dice which gives the exact same distribution of sums. How many possibilities are there? (For background, see this blog.)

• Complete the following problems.
  • 10A1.  7.8.16
  • 10A2.  7.8.19de
  • 10A3.  7.8.21 (Note that in some versions of the fourth edition, the statement is incorrect!)
  • 10A4.  7.8.35
  • 10A5.  7.8.38
• Revised poster proposal due

• (Due by bedtime Wed) Reading report on sections 7.1, 7.2, and 7.4. You may also wish to read Chapter 7.5 to prepare for the upcoming class periods.
• Complete the following problems.
  • 9B1.  7.8.9
  • 9B2.  7.8.11 (use induction)
  • 9B3.  7.8.12
  • 9B4.  7.8.15
  • 9B5.  7.8.29
  • 9B6.  7.8.37

• Complete the following problems.
  • 9A1. 6.7.16
  • 9A2. (a) 6.7.25 (b) 6.7.26
  • 9A3. 7.8.8
  • 9A4. Let a_n be the maximal number of pieces into which you can cut a circle using n straight lines. Determine the first few values of a_n. Use the online encyclopedia of integer sequences (OEIS) to determine what the formula is for a general term. On that webpage, look at the graph of the sequence and listen to the sequence. Write down the 42nd term of the sequence. Then, via the WebCam link at the bottom of the page, look through a few sequences and write down one that looks interesting and say why.
  • 9A5.  Use the monomino-domino interpretation of the Fibonacci numbers to prove that b₀+b₂+b₄+...+b_2n=b_2n+1.
    (Hint: IS THERE a last square in the tiling somewhere?)

• (Due by bedtime Wed) Reading report on sections 6.1, 6.2, 6.3, and 6.4.
• Complete the following problems.
  • 8B1.  6.7.15
  • 8B2.  6.7.17
  • 8B3.  6.7.24
  • 8B4.  7.8.1
  • 8B5.  Use the monomino-domino interpretation of the Fibonacci numbers to prove that b_m+n=b_mb_n+b_m-1b_n-1
  • 8B6.  Use the monomino-domino interpretation of the Fibonacci numbers to prove that (ⁿ₀)+(^n-1₁)+(^n-2₂)+...=b_n
  • (*) 8B7.  I opened a mini bag of skittles one day last month. There were 15 skittles, 3 of each of the five colors. What is the probability of that happening?

• Complete the following problems.
  • 8A1. (a) 5.8.5 (b) 5.8.41 (c) 5.8.39
  • 8A2. 6.7.5
  • 8A3. 6.7.11
  • 8A4. 6.7.14
  • 8A5.  Give a combinatorial proof of Equation 5.14.
    (Hint: Condition on when the last chosen element occurs.)

• (Due by bedtime Wed) Reading report on sections 5.2, 5.3, 5.5, and 5.6.
• Complete the following problems.
  • 7B1.  5.8.19
  • 7B2.  5.8.23
  • 7B3.  5.8.24
  • 7B4.  5.8.29
  • 7B5.  5.8.44
  • 7B6.  6.7.1
  • 7B7.  6.7.3

• 6S1.  2.4.6
• 6S2.  3.6.36
• 6S3.  3.6.41
• 6S4.  3.6.45
• 6S5.  5.8.5
• 6S6.  5.8.9

• Complete the following problems.
  • 6A1.  3.6.31
  • 6A2.  3.6.38
  • 6A3.  3.6.51
  • 6A4.  5.8.7
  • 6A5.  5.8.13

• (Due by 11:59pm Wed) Reading report on sections 3.4, 3.5, and 5.1.
• Complete the following problems.
  • 4B3.  3.6.22
  • 4B4.  3.6.50
  • 4B5.  3.6.54
  • 5B1.  3.6.28
  • 5B2.  3.6.43
  • 5B3.  5.8.1
  • 5B4.  5.8.11

• Read sections 3.4 and 3.5; then, complete the following problems.
  • 5A1.  3.6.9
  • 5A2.  3.6.16
  • 5A3.  3.6.19
  • 5A4.  3.6.37
  • 5A5.  3.6.39ab and 3.6.40c

• (Due by 11:59pm Wed) Reading report on sections 3.1, 3.2, and 3.3.
• Complete the following problems.
  • 4B1.  3.6.7
  • 4B2.  3.6.20
  • 4B3.  3.6.22
  • 4B4.  3.6.50
  • 4B5.  3.6.54

• Read sections 3.1 and 3.2; then, complete the following problems.
  • 4A1.  2.4.15
  • 4A2.  3.6.1
  • 4A3.  3.6.8
  • 4A4.  3.6.10
  • 4A5.  The book-designer used four fonts (thick roman, thick italic, thin roman, thin italic) and four colors (red, orange, yellow,and blue, more or less) in writing the word ``combinatorics'' on the cover subject to the constraint that adjacent letters must be different fonts and different colors. Determine the number of ways in which this may be accomplished.

• (Due by 11:59pm Wed) Reading report on sections 1.7, 2.1, and 2.2. Email chanusa@math.binghamton.edu.
• Complete the following problems.
  • 2B1.  (a) 2.4.16 (b) 2.4.17
  • 2B2.  2.4.19abc
  • 2B3.  2.4.26
  • 2B4.  2.4.27

• Read sections 1.7 and 2.1 then complete the following problems.
  • 2A1.  1.8.29
  • 2A2.  1.8.35
  • 2A3.  1.8.37
  • 2A4.  2.4.5
  • 2A5.  2.4.2
• Remember that you must explain your work and reasoning to receive full credit. I expect to see sentences and paragraphs.

• Read the syllabus. This should answer any questions you have about the course.
• (Due by 11:59pm Wed) Reading report on sections 1.0, 1.1, 1.2, and 1.5.
  • Explain in your own words four general types of combinatorial problems we may encounter in this class.
  • Complete this sentence: ``The more problems one solves...''
  • Follow the guidelines on reading reports for sections 1.1 (pp4-5), 1.2, and 1.5.
• Complete the following problems.
  • 1B1.  (a) 1.8.2 (b) 1.8.7
  • 1B2.  1.8.23 (give a heuristic about how you did it.)
  • 1B3.  (a) 1.8.26 (b) 1.8.27
  • (and determine what type(s) of combinatorial problem each of these exercises involve.)