Exam Practice Questions
Exam 2: Thursday, December 6, 2012
- Exam 2 covers the material on generating functions, recurrence relations, integer partitions, Catalan numbers, trees, combinatorial statistics and q-analogs. This includes pages 76-81, 102-139 (except the parts on EGFs), 146-150, 175-184, and 238-248 from the textbook and all pages of the notes starting with page 77. This exam is NOT cumulative. I have prepared the following questions for you to practice the material.
- We will go over any questions that you have from this problem set, Homeworks 6–9, and class notes on Question and Answer Day, Tuesday, December 4, 2012. I can also suggest the questions sprinkled throughout the text.
- Book exercises: 2.4.4, 2.4.6, 2.4.8, 3.3.5, 3.3.9 (then use convolution formula), 3.4.2, 3.4.11, 3.5.1e, 3.6.2, 3.6.6, 4.4.1, 4.4.2, 4.4.3 (Bolded exercises are especially encouraged.)
- Book questions (in the chapters): 123, 172, 174, 234, 235, 241
- Q1. We can make a four-sided die using a tetrahedron. If the sides of the die are 1, 2, 3, and
4, then there is a particular distribution of possible sums between 2 and 8. Determine a relabeling of the two dice
which gives the exact same distribution of sums. How many possibilities are there?
- Q2. The Catalan numbers cn satisfy the generating function
c(x)=Σn≥0 cnxn=(1 - sqrt(1-4x))/2.
Consider an integer sequence dn which has as its generating function
d(x)=Σn≥0 dnxn=1 - 5 sqrt(1-4x).
Determine a formula for dn in terms of the nth Catalan number, cn.
- Q3. Investigate and conjecture a formula for the number of standard Young tableaux of
shape λ: 2n=n+n there are for all positive n. For example, when n=3, two valid
tableaux are
Prove your conjecture by finding a bijection with a combinatorial interpretation we have seen previously. [Hint:
you will likely use the fact that a standard Young tableau of shape n,n is completely defined by its first
row.]
- Q4. Use a bijection to show that sequences 1 ≤ a1 ≤ a2 ≤
... ≤ an of length n, where each ai ≤ i are also counted by the
Catalan numbers. For example, when n=3, the five sequences are 111, 112, 113, 122, and 123. (Hint: Draw
the lattice paths and count the area to the left of the curve.)
- Q5. In chess, a knight can make moves of type "1 horizontal step and 2 vertical steps"
or "2
horizontal steps and 1 horizontal step". Consider the following strange chessboard:
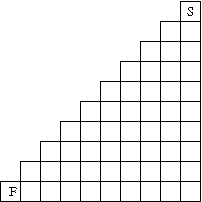 If your knight starts in the upper right corner and can only move SSW or WSW, determine how many paths
exist in order
for the knight to arrive at the bottom left corner?
If your knight starts in the upper right corner and can only move SSW or WSW, determine how many paths
exist in order
for the knight to arrive at the bottom left corner?
- Q6. In the spirit of Q5, conjecture and prove a formula for how many knight paths
there are if
the size of the triangular board is 3n+1 by 3n+1 instead of 10 by 10.
- For informational purposes only, here is a copy of a second exam from the past. No guarantees of similarity are assured. I suggest saving this for practice once you are completely prepared for the exam. Also, ignore question 2 because Inclusion/Exclusion was involved on the first exam.
- Class on 12/11 will a "fun class" about my research. On 12/13, we will have a poster work day, where you can bring in last minute questions about your project. Our poster session will be from 5-7 on Tuesday, 12/18. Let me know if you have a conflict.
OPTIONAL Homework 10 FINAL VERSION
To be turned in no later than Tuesday, December 11, 2012
- This homework is completely optional. It is NOT a "bonus" homework. If you complete this homework, I will grade it normally and it will count toward your homework grade. If you do not complete this homework, it will not impact your homework grade. Solve the following three problems, worth 7 points each.
- 10-1. 6.2.9abc
- 10-2. Find and prove a bijection between binary trees and some other interpretation of the Catalan numbers.
- 10-3. Find the compact form of the multivariate generating function f(x,y)=ΣSxnym that enumerates sets S of positive integers. The n is the number of elements in the set S and the m is the largest number in the set S.
[Hint: The sets with maximum element N are those that are subsets of N-1.]
Homework 9
To be prepared for presentation on Thursday, November 29, 2012
- Read Sections 3.4, 4.1, 6.2, and the notes on multiplication and composition of generating functions, Catalan numbers, and counting trees. You may find this handout on Catalan numbers helpful. Then solve the following problems. If you wish to present one of these questions in class, claim it upon arrival.
- 9-1. How many ways are there to take a group of n soldiers, break then into non-empty platoons, and choose some (possibly empty) subset of each platoon to be on "night watch"? Give an exact answer, not simply a generating function.
- 9-2. Determine the compact form for the generating function E(x)=Σn≥0 enxn for the sequence en defined by
e0=1, e1=1, e2=4,
and en=3cn-1+1 for n>3, where cn is the nth Catalan number.
- 9-3. (a) Find the 14 Dyck paths of length 4 and the 14 multiplication schemes for 5 variables.
(b) Use the Catalan bijections from class to determine which Dyck path corresponds to which multiplication scheme. (A Dyck path is a (0,0) to (n,n) lattice path that stays above the line y=x.)
- 9-4. Let 2n equally spaced points on a circle be chosen. Show that the number of ways to join these points in pairs so that the resulting n line segments do not intersect equals the nth Catalan number.
- 9-5. Define the Schröder number sn to be the number of paths from (0,0) to (n,n) with steps (1,0), (1,1), and (0,1) that stay above the line y=x. Find the generating function S(x)=Σn≥0 snxn.
- 9-6. (a) How many different labeled trees are there on seven vertices? (b) How many different unlabeled trees are there on seven vertices?
Homework 8
To be turned in on Tuesday, November 20, 2012
- Read Sections 2.4, 3.4, and 4.4. Then solve the following four problems, worth five points each.
- 8-1. 4.1.10
- 8-2. 4.1.13
- 8-3. (a) Determine the generating function for the number of partitions of n such that there are at most two parts of the same size. (4111 is not allowed since 1 appears thrice.)
(b) Prove that the number of partitions of n in which no part occurs more than three times equals the number of partitions of n in which no part is divisible by 4.
- 8-4. This question is related to the number of standard Young tableaux of the partition λ=(n-k)+1+1+1+...+1, which has one part of size n-k and k parts of size 1. (This is a partition of the integer n.)
(a) Determine the number of standard Young tableaux of shape λ using the hook length formula.
(b) Determine the number of standard Young tableaux of shape λ without using the hook length formula—count them directly.
- Reminder: Your poster outline is due Thursday, November 15.
Homework 7
To be prepared for presentation on Thursday, November 1, 2012 Tuesday, November 6, 2012
- Read Sections 3.3–3.6 (except the topics on exponential generating functions). Then solve the following problems. If you wish to present one of these questions in class, claim it upon arrival.
- 7-1. 3.3.2
- 7-2. 3.3.3
- 7-3. 3.5.1c
- 7-4. 3.5.1d [Hint: The partial fractions expansion of (ax+b)/(1-cx)^2 has the form A/(1-cx)+B/(1-cx)^2.]
- 7-5. 3.5.5
- 7-6. (a) Determine the generating function for the number of partitions of n such that there are at most two parts of the same size. (4111 is not allowed since 1 appears thrice.)
(b) Determine the generating function for the number of partitions of n such that the parts are all of size equal to a power of two. (Example: 844221.)
- We will discuss solutions to these questions in class. There will also be time for discussion of any questions you may have from class.
- Reminder: Your poster proposal is also due Thursday, November 1.
Half-Homework 6
To be turned in on Thursday, October 25, 2012
- Read Section 3.3. Then solve the following two problems, each worth five points.
- 6-1. Prove that the sum from j=2 to infinity of [1 over (j2)] equals 2.
[Hint: Write the denominator as a polynomial of j, then use partial fractions]
- 6-2. Verify the following equation AND use it to determine how many ways there are to score 100 points in basketball.
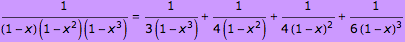
- Reminder: Your poster proposal is due on Thursday, November 1.
Exam Practice Questions
Exam 1: Tuesday, October 16, 2012
- Exam 1 covers the material from Sections 1.1–1.4 and 2.1–2.4 (through p. 77), 3.1, 4.2 (square-domino Fibonacci interpretation) and class 10/9. I have prepared the following questions for you to practice the material.
- We will go over any questions that you have from this problem set, Homeworks 1–5, and class notes on Question and Answer Day, Monday, October 17, 2011. I can also suggest the questions sprinkled throughout the text.
- Book exercises: 1.2.6, 1.2.9, 1.3.5, 1.3.12, 1.4.8, 2.1.3, 2.1.13, 2.2.7cdf, 2.3.1, 2.3.4, 2.3.6 2.4.1, 2.4.5, 2.4.11, (Bolded exercises are especially encouraged.)
- Book questions (in the chapters): Q40 (p37), Q43 (p38)
- Practice this web quiz on functions.
- P1. Write down a list of all combinatorial interpretations of (n choose k) and (n multichoose k) from the book.
- P2. Use the square-domino interpretation of the Fibonacci numbers to prove
that fm+n=fmfn+fm-1fn-1
- P3. There are many games that have a combinatorial flavor. One of these games is Tantrix. Tantrix tiles have six sides (they're hexagonal); on each tile there are three colored paths (using three out of the four colors red, yellow, green, and blue). These paths leave one of the six sides of the tile and arrive at some other side of the tile. Determine the possible number of tiles that satisfy these criteria. [Hint: draw all possible ways that three pairs of two sides can be paired up. Then figure out in how many ways they can be colored (realizing that rotations may define some sort of equivalence class. Last, realize that the answer is not 56 (the number of tiles in a Tantrix set) because there are a few valid tiles that are not included.]
- For informational purposes only, here is a copy of a first exam from the past. No guarantees of similarity are assured. I suggest saving this for practice once you are completely prepared for the exam. Also, ignore question 1 because you did not learn this material.
- Reminder: Your poster proposal is due on November 1.
Half-Homework 5
To be turned in on Thursday, October 11, 2012
- Read Section 3.1 and Section 4.2 on the square-domino interpretation of the Fibonacci numbers. Then solve the following two problems, each worth five points.
- 5-1. 3.1.10
- 5-2. Use the square-domino interpretation of the Fibonacci numbers to prove
that f2n=1+Σni=1 f2i-1.
Homework 4
To be prepared for presentation on Thursday, October 4, 2012
- Read Sections 2.1–2.4 (through page 77) and the notes on combinatorial proofs. Then solve the following problems. If you wish to present one of these questions in class, claim it upon arrival. (If you have already presented, please let others present this time.)
- 4-1. Answer the following jeopardy questions by giving a "real world" situation that could be counted by the given quantity: 1.2.1abcd, 2.1.1abc, 2.2.1abcd
- 4-2. Present Combinatorial Proof #2 on p.55 and explain the answers to Questions 62 and 63.
- 4-3. 2.2.5 [Hint: See Exercise 2.2.4c]
- 4-4. (a) Exercise 2.2.4a
(b) Now, prove this formula using the binomial theorem.
- 4-5. 2.3.6
- 4-6. 2.3.11
- We will discuss solutions to these questions in class. There will also be time for discussion of any questions you may have from class.
Homework 3
To be turned in on Thursday, September 27, 2012
- Read Sections 2.1–2.2. Then solve the following problems.
- 3-1. (a) How many set partitions of [n] into two blocks are there? (Definition of block on p. 35)
(b) How many set partitions of [n] into (n-1) blocks are there?
(c) How many set partitions of [n] into (n-2) blocks are there?
- 3-2. (a) Let f be a well-defined function from A to B and let g be a well-defined function from B to A. Suppose that g(f(a))=a for all a in A. Show that it is not necessarily the case that f is a bijection between A and B.
(b) Let f be a well-defined function from A to B and let g be a well-defined function from B to A. Suppose that g(f(a))=a for all a in A and f(g(b))=b for all b in B. Prove that f is a bijection between A and B. (Use the definition of bijection.)
- 3-3. (a) Use the equivalence principle to solve Exercise 1.4.15.
(b) Write a paragraph explaining why we can not use the equivalence principle to count the number of different necklaces where two of the n beads are indistinguishable (the same color, for example).
- 3-4. Exercise 2.1.4
- 3-5. Exercise 2.1.12
Homework 2
To be prepared for presentation on Thursday, September 13, 2012
- Read Sections 1.1–1.4. Then solve the following problems. If you wish to present one of these questions in class, claim it upon arrival.
- 2-1. 1.2.4abcde
- 2-2. (a) 1.2.16
- 2-3. In chess, a rook is a piece that can move only vertically and horizontally. Therefore, two rooks attack each other if they are placed in the same row or in the same column. A non-attacking configuration of rooks consists of placing some number of rooks on a chessboard so that no pair of rooks attack each other. Determine the number of non-attacking configurations of five indistinguishable rooks on an 8x8 chessboard.
- 2-4. In the following problem, suppose k≤n.
(a) How many functions are there from [k] to [n]?
(b) How many one-to-one functions are there from [k] to [n]?
(c) How many onto functions are there from [k] to [n]?
(d) How many bijections are there from [k] to [n]?
- 2-5. Create a bijection between two-member subsets of {1, 2,..., n, n+1} and all possibilities of placing one pair of parentheses in a string of n letters. For example, if n were three, we see that there are six two-member subsets of {1,2,3,4} and there are six ways to place one pair of parentheses in the word abc: (a)bc, (ab)c, (abc), a(b)c, a(bc), and ab(c). Notice that a()bc is not valid---there are no letters between the parentheses.
- 2-6. 1.4.6
- We will discuss solutions to these questions in class. There will also be time for discussion of any questions you may have from class.
Homework 1
To be turned in on Thursday, September 6, 2012
- Thoroughly read the class web page including the syllabus and schedule. This should answer all the questions that you may have about the class. Read Sections 1.1 and 1.2.
- Problem 1-1 must be completed online before class on
Wednesday Thursday 9/6 for credit.
- 1-1. (a) Email me at chanusa@qc.cuny.edu with the email address where you are best contacted. (Make sure to include your name in the message as well!) Also, if you are a QC undergraduate, please include your expected graduation year.
(b) Take the syllabus quiz on Blackboard. Retake the quiz as necessary to earn a score of 100%.
- Problems 1-2 through 1-5 should be written up and handed in in class before class starts on Thursday: [Remember to explain all your work!!!]
- 1-2. 1.1.2ab (This means Parts a and b in Problem 2 of Section 1.1)
And: (c) Assuming that the coin is fair, what is the probability that a sequence of 20 flips has exactly 10 heads and 10 tails?
- 1-3. (a) 1.1.5 (b) Consider all ways to choose fifteen coins and the amount of money each way represents. (For example, 15 dimes equals $1.50.) What is the smallest amount of money that occurs in at least two different ways?
- 1-4. 1.1.15.
- 1-5. 1.2.3
- Remember what is expected:
- When the problem says give an example of an object with property a, you need to give such an object and explain why it satisfies a.
- When the problem says "Prove X" or "Show X", you need to give a rigorous mathematical argument explaining why "X" is true.
- Write your solutions using complete sentences.
- Follow the guidelines for turning in homework.
|