Exam Practice Questions
Exam 2: Wednesday, December 7, 2011
- Exam 2 covers the material from Sections 2.4, 3.1, 3.3–3.5 (ignoring topics on EGFs), 4.2, 4.4, and 6.2, and the material on Catalan numbers and standard Young tableaux. I have prepared the following questions for you to practice the material.
- We will go over any questions that you have from this problem set, Homeworks 6–9, and class notes on Question and Answer Day, Monday, December 5, 2011. I can also suggest the questions sprinkled throughout the text.
- Book exercises: 2.4.4, 3.1.10, 3.3.5, 3.4.2, 3.4.11, 3.5.1e, 3.6.2a, 4.1.12, 4.2.1, 4.2.2, 4.4.3, 6.3.9 (Bolded exercises are especially encouraged.)
- Book questions (in the chapters): 123, 172, 174, 234, 235, 241
- Q1. Use the square-domino interpretation of the Fibonacci numbers to prove
that fm+n=fmfn+fm-1fn-1
- Q2. We can make a four-sided die using a tetrahedron. If the sides of the die are 1, 2, 3, and
4, then there is a particular distribution of possible sums between 2 and 8. Determine a relabeling of the two dice
which gives the exact same distribution of sums. How many possibilities are there?
- Q3. The Catalan numbers cn satisfy the generating function
c(x)=Σn≥0 cnxn=(1 - sqrt(1-4x))/2.
Consider an integer sequence dn which has as its generating function
d(x)=Σn≥0 dnxn=1 - 5 sqrt(1-4x).
Determine a formula for dn in terms of the nth Catalan number, cn.
- For informational purposes only, here is a copy of a second exam from the past. No guarantees of similarity are assured. I suggest saving this for practice once you are completely prepared for the exam. Also, ignore question 2 because you did not learn this material.
Optional Homework 9
To be turned in before class on Monday, December 5, 2011. (No grace days may be used because we may discuss these problems in class.)
- This is an optional homework assignment. If you complete this assignment, the grade you receive will count toward your homework grade. If you do not complete this assignment, your homework grade will be based on your homework assignments to date.
- There are only three questions in this homework.
- 9-1. Show that the number of Ferrers diagrams that fit inside an m by n rectangle is (m+nm). (Hint: look for a bijection with walks in a lattice.)
- 9-2. 3.6.6
- 9-3. (a) Find the 14 Dyck paths of length 4 and the 14 multiplication schemes for 4 variables.
(b) Use the Catalan bijections from class to determine which Dyck path corresponds to which multiplication scheme. (A Dyck path is a (0,0) to (n,n) lattice path that stays above the line y=x.)
Homework 8
To be prepared for presentation on Monday, November 28, 2011
- Read Sections 3.5 (skip parts on EGFs), 2.4, 3.4, and 4.4. Then solve the following problems. If you wish to present one of these questions in class, claim it upon arrival.
- 8-1. 3.5.1c
- 8-2. 3.5.1d [Hint: The partial fractions expansion of (ax+b)/(1-cx)^2 has the form A/(1-cx)+B/(1-cx)^2.]
- 8-3. Prove that the number of partitions of n in which no part occurs more than three times equals the number of partitions of n in which no part is divisible by 4.
- 8-4. This question is related to the number of standard Young tableaux of the partition λ=(n-k)+1+1+1+...+1, which has one part of size n-k and k parts of size 1. (This is a partition of the integer n.)
(a) Determine the number of standard Young tableaux of shape λ using the hook length formula.
(b) Determine the number of standard Young tableaux of shape λ without using the hook length formula—count them directly.
- 8-5. Explain the proof of Theorem 4.2.4.
- 8-6. 4.1.13
Homework 7
To be turned in on Wednesday, November 9, 2011 (Now due Monday, November 14.)
- Read Sections 3.3 and 3.4. Then solve the following problems.
- 7-1. 3.1.4ab
- 7-2. Prove that the sum from j=2 to infinity of [1 over (j2)] equals 2.
[Hint: Write the denominator as a polynomial of j, then use partial fractions]
- 7-3. 3.3.7 [Hint: Multiply out some generating functions.]
- 7-4. (a) Determine the generating function for the number of partitions of n such that there are at most two parts of the same size. (4111 is not allowed since 1 appears thrice.)
(b) Determine the generating function for the number of partitions of n such that the parts are all of size equal to a power of two. (Example: 844221.)
- 7-5. Verify the following equation AND use it to determine how many ways there are to score 100 points in basketball.
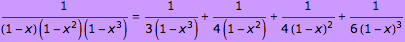
- Reminder: Your revised poster proposal is also due on November 9.
Homework 6 (Final Version; Updated 24 October 2011)
To be prepared for presentation on Wednesday, November 2, 2011
- Reminder: Your poster proposal is also due on November 2. (Not October 26 as written earlier on this site.)
- Read Sections 3.1 and 3.3 and skim section 3.2. Then solve the following problems. If you wish to present one of these questions in class, claim it upon arrival.
- 6-1. 3.1.5
- 6-2. 3.1.8
- 6-3. 3.1.17(a) [Feel free to try (b)]
- 6-4. 3.2.6
- 6-5. 3.3.2acf
- 6-6. 3.3.3bde
Exam Practice Questions
Exam 1: Wednesday, October 19, 2011
- Exam 1 covers the material from Sections 1.1–1.4 and 2.1–2.4. I have prepared the following questions for you to practice the material.
- We will go over any questions that you have from this problem set, Homeworks 1–5, and class notes on Question and Answer Day, Monday, October 17, 2011. I can also suggest the questions sprinkled throughout the text.
- Book exercises: 1.2.6, 1.2.9, 1.3.5, 1.3.12, 1.4.6, 1.4.8, 2.1.13, 2.2.7cdf, 2.3.1, 2.3.4, 2.3.6 2.4.1, 2.4.5, 2.4.11, (Bolded exercises are especially encouraged.)
- Book questions (in the chapters): Q40 (p37), Q43 (p38)
- Practice this web quiz on functions.
- P1. Write down a list of all combinatorial interpretations of (n choose k) and (n multichoose k) from the book.
- P2. Create a bijection between two-member subsets of {1, 2,..., n, n+1} and all possibilities of placing one pair of parentheses in a string of n letters. For example, if n were three, we see that there are six two-member subsets of {1,2,3,4} and there are six ways to place one pair of parentheses in the word abc: (a)bc, (ab)c, (abc), a(b)c, a(bc), and ab(c). Notice that a()bc is not valid---there are no letters between the parentheses.
- P3. There are many games that have a combinatorial flavor. One of these games is Tantrix. Tantrix tiles have six sides (they're hexagonal); on each tile there are three colored paths (using three out of the four colors red, yellow, green, and blue). These paths leave one of the six sides of the tile and arrive at some other side of the tile. Determine the possible number of tiles that satisfy these criteria. [Hint: draw all possible ways that three pairs of two sides can be paired up. Then figure out in how many ways they can be colored (realizing that rotations may define some sort of equivalence class. Last, realize that the answer is not 56 (the number of tiles in a Tantrix set) because there are a few valid tiles that are not included.]
- For informational purposes only, here is a copy of a first exam from the past. No guarantees of similarity are assured. I suggest saving this for practice once you are completely prepared for the exam. Also, ignore question 1 because you did not learn this material.
- Reminder: Your poster proposal is due on Wednesday,
October 26 November 2.
Half-Homework 5
To be turned in on Wednesday, October 12, 2011
- Read Sections 2.1–2.2. Then solve the following two problems, each worth five points.
- 5-1. 2.1.3
- 5-2. (a) Exercise 2.2.4a
(b) Now, prove this formula using the binomial theorem.
Homework 4
To be prepared for presentation on Wednesday, October 5, 2011
- Read Sections 2.1–2.2. Then solve the following problems. If you wish to present one of these questions in class, claim it upon arrival.
- 4-1. Answer the following jeopardy questions by giving a "real world" situation that could be counted by the given quantity: 1.2.1abcd, 2.1.1abc, 2.2.1abcd
- 4-2. Present Combinatorial Proof #2 on p.55 and explain the answers to Questions 62 and 63.
- 4-3. 2.2.5 [Hint: See Exercise 2.2.4c]
- 4-4. 2.1.12
- 4-5. 2.1.13
Homework 3
To be turned in on Monday, September 26, 2011
- Read Sections 1.3 and 1.4. Then solve the following problems. If you wish to present one of these questions in class, claim it upon arrival.
- 3-1. Find and prove a bijection between the set of all functions from [n] to [3] and
the set of all integers from 1 to 3n.
- 3-2. (a) How many set partitions of [n] into two blocks are there?
(b) How many set partitions of [n] into (n-1) blocks are there?
(c) How many set partitions of [n] into (n-2) blocks are there?
- 3-3. Exercise 1.4.10.
- 3-4. (a) Use the equivalence principle to solve Exercise 1.4.15.
(b) Write a paragraph explaining why we can not use the equivalence principle to count the number of different necklaces where two of the n beads are indistinguishable (the same color, for example).
- 3-5. Exercise 2.1.6abc (You can solve this with tools from Chapter 1.)
Homework 2
To be prepared for presentation on Monday, September 19, 2011
- Read Sections 1.1–1.3. Then solve the following problems. If you wish to present one of these questions in class, claim it upon arrival.
- 2-1. 1.1.15
- 2-2. 1.2.4abcde
- 2-3. In chess, a rook is a piece that can move only vertically and horizontally. Therefore, two rooks attack each other if they are placed in the same row or in the same column. A non-attacking configuration of rooks consists of placing some number of rooks on a chessboard so that no pair of rooks attack each other. Determine the number of non-attacking configurations of five indistinguishable rooks on an 8x8 chessboard.
- 2-4. In the following problem, suppose k≤n.
(a) How many functions are there from [k] to [n]?
(b) How many one-to-one functions are there from [k] to [n]?
(c) How many onto functions are there from [k] to [n]?
(d) How many bijections are there from [k] to [n]?
- 2-5. 1.3.13
- We will discuss solutions to these questions in class. There will also be time for discussion of any questions you may have from class.
Homework 1
To be turned in on Monday, September 12, 2011
- Thoroughly read the class web page including the syllabus and schedule. This should answer all the questions that you may have about the class. Read Sections 1.1 and 1.2.
- Problem 1-1 must be completed online before class on Monday 9/12 for credit.
- 1-1. (a) Email me at chanusa@qc.cuny.edu with the email address where you are best contacted. (Make sure to include your name in the message as well!)
(b)Take the syllabus quiz on Blackboard. Retake the quiz as necessary to earn a score of 100%.
- Problems 1-2 through 1-5 should be written up and handed in in class before class starts on Wednesday:
- 1-2. Exercise 1.1.9 abc (This means Exercise 9 in Section 1.1, parts a, b, and c)
- 1-3. Exercise 1.1.6
- 1-4. Exercise 1.1.14
- 1-5. Exercise 1.2.18 abcdefghij
- Remember what is expected:
- When the problem says give an example of an object with property a, you need to give such an object and explain why it satisfies a.
- When the problem says "Prove X" or "Show X", you need to give a rigorous mathematical argument explaining why "X" is true.
- Write your solutions using complete sentences.
- Follow the guidelines for turning in homework.
|