Graph Theory Spring 2011
Home Page
Syllabus
Calendar
Homework
Guidelines
Letters
Notes
Project
List
  
 
Christopher Hanusa > Courses > Graph Theory Spring 2011 > Homework
 
Homework
Graph Theory – Spring 2011
Midterm Practice (Not to be turned in)
  • Midterm: Monday, May 23, 2011 from 4pm-6pm
  • The midterm covers Sections 7.1-7.2, 8.1-8.3, 9.1, and various graph algorithms.  (See notes for detail.)
  • In preparation for the midterm, I have compiled some practice problems which you can practice before the Q&A session in class on Wednesday, May 18. You will also want to check out Optional Homework 9 below.
    • 7.1.2, 7.1.3, 7.1.8, 7.2.1, 8.1.10, 8.1.16, 8.3.7
    • Q1.  Find a graph that has two non-isomorphic planar duals. [Hint: Look for different planar embeddings.]
    • Q2.  Find and prove an "Euler's formula" for disconnected planar graphs.
    • Q3.  With four men and four women, find sets of preferences for the men and women such that running the Gale-Shapley algorithm with the men proposing and then with the women proposing gives two different sets of marriages. Show that your answers illustrate the optimality/pessimality of the algorithm.
    • Q4.  Find the size of a maximum matching in the cycle Cn and the wheel Wn.
    • Q5.  Find the minimum weight Traveling Salesman tour of the weighted graph from Figure 7.1.7. Justify that your answer is correct.
  • For informational purposes only, here is a copy of a second exam from the past. No guarantees of similarity are assured.  The topics from that exam are slightly different than what you have seen.
  • You should also go over your past homework problems.
  • Also to keep in mind: Your project revision is due Monday, May 23.
Optional Homework 9
To be turned in on: Wednesday, May 18, 2011, no later than 4:30pm.  This homework is optional.  If you turn it in, it will count toward your grade.  If you do not turn it in, it will not count toward your grade.
  • Read Section 7.1. Try examples of all the algorithms we did in class. Then answer the following questions, each worth five points:
    • 9-1.  Find the max flow and min cut in this network: (PDF)
    • 9-2.  (a) Complete problem 7.1.10 (b) What is the maximum possible weight of a minimum weight spanning tree of the cube graph using edges of weight 1,1,1,1,2,2,2,2,3,3,3,3? (as in part (a))
    • 9-3.  Prove that if all the edge costs are different, then there is only one minimum-weight spanning tree.
    • 9-4.  You wish to leave from New York City on a cross-country tour, returning to New York after visiting once each the following cities: Boston, Chicago, Detroit, Denver, Houston, Los Angeles, Miami, Minneapolis, St Louis, San Francisco, Seattle, and Washington DC. Use the approximation algorithm from class to find a Hamiltonian cycle through these fourteen cities. You may find this website useful.
Homework 8
To be prepared for presentation on: Wednesday, May 11, 2011.
  • Read Sections 7.2 and the course notes on max flow/min cut. Then answer the following four questions:
    • 8-1.  Practice network flow on this network.
    • 8-2.  Run the Gale-Shapley algorithm with the following sets of preferences with the women proposing:
      Women's Preferences

      		April Bettie Carol Delphi Eve
      1st Choice F F G G H
      2nd Choice G H I H F
      3rd Choice I I F J I
      4th Choice J G H I G
      5th Choice H J J F J
       
      Men's Preferences

      		Freddie Greg Harold Isaac Joe
      1st Choice C E A E B
      2nd Choice B B D C D
      3rd Choice E C B A A
      4th Choice A A E B C
      5th Choice D D C D E
    • 8-3.  The market for kumquats is booming!
      Five markets (I through V) each have put orders into the five large kumquat distributors (A through E).
      A has 5 kumquats and can deliver to I, II, and III.
      B has 4 kumquats and can deliver to I, III, and IV.
      C has 2 kumquats and can deliver to II and III.
      D has 5 kumquats and can deliver to III and V.
      E has 4 kumquats and can deliver to IV and V.
      Market I desires 5 kumquats, II desires 2, III desires 4, IV desires 6, and V desires 3.
           Is it possible for all the markets to receive their desired quantity of kumquats for the distributors? If so, give a valid transshipment. If not, explain why not.
    • 8-4.  Suppose that you have a network G with multiple sources and multiple sinks. Describe how to modify G so that we can apply the Ford-Fulkerson algorithm in order to find a maximum flow from all sources to all sinks.
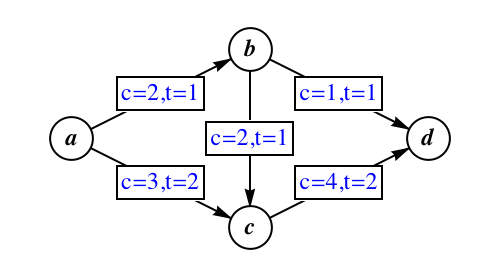
    • 8-5.  Determine the maximum flow from a to d from time 0 to time 4 in the following dynamic network:
Homework 7
To be turned in on: Monday, May 2, 2011.
  • Read Sections 9.1, 8.2, and 8.3. Then answer the following questions:
    • 7-1.  Use an argument involving girth to prove that the Petersen graph is not planar.
    • 7-2.  This question has to do with planar duality:
      (a) Show that for all n, the wheel graph Wn is self-dual. (Give the isomorphism which proves that the dual graph is isomorphic to the original.)
      (b) Show that the planar dual of the octohedron is the cube and vice versa.
    • 7-3.  Prove that the graph G in Figure 9.1.19 (p. 190) is non-planar using two methods:
      (a) Find a subdivision of K3,3 or K5 that is a subgraph of G.
      (b) Through a series of edge deletions and edge contractions, show that either K3,3 or K5 is a minor of G.
    • 7-4.  A spanning tree T in a connected graph G is a subgraph of G that is a tree and includes every vertex of G. (See also p.20 and Section 7.1 in the book.) Prove the correctness of the following algorithm to find a spanning tree of a graph. [Prove that the algorithm terminates and that the output of the algorithm is a spanning tree of G.]
      Input: A graph G with n vertices.
      Preprocess: Label the vertices 1 through n, color them all white. Let T be a set of edges, initially empty.
      Repeat: For the lowest numbered white vertex v, order the edges incident with v. Going through each edge e from first to last, determine if including e in T would create a cycle in T. If it would not create a cycle, place e into T (T is growing.) If it would create a cycle, do not add e to T; go on to the next edge. Once every incident edge to v has been checked, color v black. If all vertices are black, go on to the next step. Otherwise, repeat this step.
      Output: Output the graph T, a spanning tree of G.
    • 7-5.  Use the Hungarian algorithm to solve problem 7.2.2.
              Important: Use the initial matching (a,4); (c,6); (e,2); (h,5).
  • Also to keep in mind: Your revised project is due to be turned in on Wednesday, May 4.
Homework 6
To be prepared for presentation on: Wednesday, April 6, 2011.
  • Read Sections 8.1, 8.2, and 8.3. Then answer the following questions:
    • 6-1.  8.1.9abc [In part (c), add edges---do not subtract them.]
    • 6-2.  8.1.14
    • 6-3.  (a) 8.2.3 and (b) 8.2.4
    • 6-4.  Show that K3,3 is a minor of the graph from Midterm Practice Problem P2.
    • 6-5.  Try to prove the Four Color Theorem by emulating the argument from class using Kempe Chains. What goes wrong?
    • 6-6. (Bonus)  Play the planarity game (See also: http://www.planarity.net/).
      Complete levels 1-4 for two bonus points and complete levels 1-7 for two more (four total). If possible, print out the level you complete and your score and turn it in on Wednesday.
  • Also to keep in mind: Your project final draft is due Wednesday, April 13.
Midterm Practice (Not to be turned in)
  • Midterm: Wednesday, March 23, 2011
  • The midterm covers Sections 1.1–1.3, 2.1–2.3, 3.1, and knight's tours.  (See notes for detail.)
  • In preparation for the midterm, I have compiled some practice problems.
    • 1.1.17, 1.2.1, 1.3.2, 1.3.16, 2.1.3, 2.1.6, 2.2.3, 2.2.5, 3.2.8
    • P1.  Prove that at a party with 49 people, there is always a person who knows an even number of others. [Assume acquaintence is mutual.]
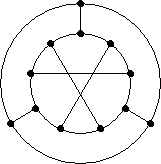
    • P2.  Determine and prove the chromatic and edge chromatic number for this graph:
    • P3.  For some k greater than or equal to 2, find a k-regular graph that has a bridge.
    • P4.  Figure 2.3.5 is on page 40 of the book. (a) Prove that Figure 2.3.5 has no Hamiltonian cycle. (b) Show that Figure 2.3.5 has a Hamiltonian path.
  • For informational purposes only, here is a copy of a first exam from the past. No guarantees of similarity are assured.  The topics from that exam are slightly different than what you have seen.
  • You should also go over your past homework problems.
  • Also to keep in mind: Your project outline is due Wednesday, March 30.
Homework 5
To be turned in on Wednesday, March 16, 2011
  • Read Sections 2.3 and 3.1. Then complete the following problems.
    • 5-1.  Prove that no perfect matching exists for each of the graphs shown in Figure 2.2.6 on page 34.
    • 5-2.  Explore Theorem 2.3.2—draw out K10 and find the 4 Hamiltonian cycles and 1 1-factor that are guaranteed by the theorem.
    • 5-3.  Exercise 2.3.22 on page 43.
    • 5-4.  (a) Prove that there is no closed knight's tour on the 3x8 grid, without simply citing the theorem from class.
              (b) Find a closed knight's tour for the 3x10 grid. (Alternatively, find an open knight's tour for half a point less.) [Hint: First find the forced edges and try not to form any small cycles.]
    • 5-5.  (a) Find a graph E which has an Eulerian circuit but no Hamilton cycle.
              (b) Find a graph H which has a Hamilton cycle but no Eulerian circuit.
      [If either is impossible, prove why you can not find such a graph.]
Homework 4
To be prepared for presentation on: Wednesday, March 9, 2011
  • Read Sections 2.2 and 2.3. Then complete the following problems.
    • 4-1.  Determine the chromatic number and edge chromatic number of the Sierpinski Graph of order n. Prove your result by induction.
    • 4-2.  2.1.4, 2.1.5
    • 4-3.  2.1.15
    • 4-4.  2.4.1, 2.4.2
    • 4-5.  Determine how many different Hamiltonian cycles there are in (a) Kn. (b) Wn.
      [Assume the vertices are labeled; two Hamiltonian cycles are different if they use different edges.]
    • 4-6.  Sudoku is sooo 2010! Solve this Hashi puzzle.
      Instructions: Edges connecting the circles (vertices) must be either vertical or horizontal. Up to two edges may be drawn connecting the same circles. The edges drawn may not cross, and the degree of each vertex is the enclosed number. Also, the entire graph must be connected!
             For many more Hashi puzzles and other fun games, visit Hashi puzzles or Puzzle Bridges
Homework 3
To be turned in on Wednesday, March 2, 2011
  • Read Sections 2.1 and 2.2. Then complete the following problems.
    • 3-1.  Is Figure 2.1.5 critical? Justify. (Don't believe everything you read!)
    • 3-2.  2.1.3
    • 3-3.  Determine (and prove) the chromatic number and edge chromatic number of the dodecahedron graph.
    • 3-4.  2.1.17
    • 3-5.  (a) Prove or disprove: If H is a subgraph of G, then χ'(H)≤χ'(G). (b) Prove or disprove: The graph K4 is a snark.
Homework 2
To be prepared for presentation on: Wednesday, February 16, 2011
  • Read Sections 1.2 and 1.3. Then complete the following problems.
    • 2-1.  Prove Lemma B.
    • 2-2.  Find two graphs with the same degree sequence, one of which is a tree and one of which is not.
    • 2-3.  1.2.10 (The conclusion of your argument should be that all three graphs are isomorphic to each other.)
    • 2-4.  Let G be a connected regular graph with 22 edges.  How many vertices CAN G have?
    • 2-5.  Prove that if n is large enough, then the following statement is true:
      For all graphs on n vertices, either G or Gc contains a cycle.
      For which n does this start to be true?
    • 2-6.  Draw the Schlegel diagram for two of the following polyhedra: Icosidodecahedron, Truncated Icosahedron, Rhombicuboctahedron, Snub Cube. (You will have to do some investigating to determine what these polyhedra are.)
Homework 1
To be turned in on Wednesday, February 9, 2011
  • Thoroughly read the class web page including the syllabus and schedule. This should answer all the questions that you may have about the class. Read Sections 1.1 and 1.2 to page 16.
  • Problem 1-1 must be completed online before class on Wednesday 2/9 for credit.
    • 1-1.  (a) Email me at chanusa@qc.cuny.edu with the email address where you are best contacted. (Make sure to include your name in the message as well!)
      (b)       Take the syllabus quiz on Blackboard. Retake the quiz as necessary to earn a score of 100%.
      (c)       Update your email address on the CUNY First system and on Blackboard to be the one where you are best contacted.
  • Problems 1-2 through 1-5 should be written up and handed in in class before class starts on Wednesday:
    • 1-2. Write a paragraph or two giving an example of where you have seen graphs in real life. (Do not use the examples from class unless you have a unique perspective.) Explain what in your example corresponds to the abstract concepts of vertices, edges, and vertex degree.
    • 1-3.  Exercise 1.1.5 (This means Exercise 5 in Section 1.1)
    • 1-4.  Exercise 1.1.4.   If you determine that the sequence is graphic, draw a graph with the given degree sequence. If you determine that the sequence is not graphic, prove it.
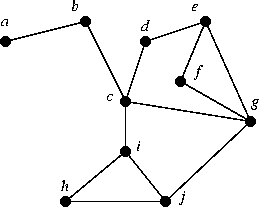
    • 1-5.  Explore the proof of Theorem 1.1.2:
      The graph below has degree sequence (S1) 4 4 3 3 3 2 2 2 2 1. Define (S2) to be 3 2 2 2 2 2 2 2 1. Walk through the steps of the proof of Theorem 1.1.2 in the following way.
      1. Let us choose vertex c from the graph to be vertex S from the proof. Next, assign to each of the remaining vertices (a – j) a (new) name of the form Ti or Di, just as in the proof.
      2. If you delete vertex S, does the new graph have degree sequence (S2)?
      3. Use the method in the proof to modify the original graph (possibly applying the algorithm multiple times) so that the resulting graph is such that removing S gives a graph with degree sequence (S2).
  • Remember what is expected:
    • When the problem says "Find a graph with property A", you need to draw the graph and explain why the graph has the property you claim it does.
    • When the problem says "Prove X" or "Show X", you need to give a rigorous mathematical argument explaining why "X" is true.
    • It may be the case that an example or a counterexample of a graph is the key to your rigorous mathematical proof. If this is the case, you will need to explain why you have drawn it and what purpose it serves.
    • Write your solutions using complete sentences.
    • Follow the guidelines for turning in homework.
Back to the Graph Theory Home Page
Christopher Hanusa – Queens College – Mathematics Department.