Homework
Math 381
Spring 2006
NOTE! Refresh your browser to get updates!
Course Schedule and a list of topics covered
Homework 15S
Special Practice Homework
- Exam 3: Wednesday, May 17, 2006, in FA 212. (NOT 209)
- Extra Office Hours: Friday, May 12, 1:30-4pm
- In preparation for the exam, I have compiled some practice problems.
- Try examples of all the algorithms we did in class.
- 15S1. Give an example of a d-regular graph with an even number of vertices that does
not have a perfect matching for d greater than or equal to three. (Similar to 14A4.)
- 15S2. What is the maximum possible weight of a minimum weight spanning tree of the cube graph using
edges of weight 1,1,1,1,2,2,2,2,3,3,3,3? (as in problem 7.1.10)
- You should also go over your past homework problems.
Homework 15A
Wednesday, May 10, 2006
- Fill out the SOOT form online!
- Ask a question about the previous weeks on a Blackboard
discussion board.
- Complete the following problems.
- 15A1. 5.3.2
- 15A2. Find the max flow and min cut in this network: (PDF)
- 15A3. Find the max flow and min cut in the second network from class (that we didn't finish). [If
you need or would like another copy, I have some outside my office door, LN 2233.]
- 15A4. The market for kumquats is booming!
Five markets (I through V) each have put orders into the
five large kumquat distributors (A through E).
A has 5 kumquats and can deliver to I, II, and III.
B has 4 kumquats and can deliver to I, III, and IV.
C has 2 kumquats and can deliver to II and III.
D has 5 kumquats and can deliver to III and V.
E has 4 kumquats and can deliver to IV and V.
Market I desires 5 kumquats, II desires 2, III desires 4, IV desires 6, and V desires 3.
Is it possible for all the markets to receive their desired quantity of
kumquats
for the distributors? If so, give a valid transshipment. If not, explain why not.
It is possible to use max flow/min cut to determine a vertex cover in a bipartite
graph.
(Remember a vertex cover is a set of vertices that is adjacent to every edge in the graph.) Given a bipartite
graph G with bipartition V=X union Y, set up a network like we did in class: create a
super-source s that is adjacent to all vertices in X and a super-sink t that is
adjacent from all vertices in Y. Next, assign capacities to all edges: for the edges you added,
give them capacity 1; for the edges of the original graph, give them capacity infinity. Now run the
Ford-Fulkerson algorithm on this graph to determine a max flow x* and min cut
S*. The set of vertices S* contains some vertices V of X and
some vertices W of Y. Prove that the set [(X\V) union W] is a vertex cover of
G. [Note: you will need to show that every edge in G is adjacent to some vertex in this
set.]
Homework 14B
May 4, 2006
- Fill out the SOOT form online!
- (Remember that your final report is to be turned in via Blackboard on Friday.)
- Read Sections 5.1 and 5.3 and this
webpage and complete the following problems.
- 5.3.3, 5.3.7, 5.3.8, 5.3.11
- 14B1. Prove that the Gale-Shapley algorithm is female-pessimal when run with the men proposing.
- 14B2. With four men and four women, find two sets of preferences such that running the
Gale-Shapley algorithm with the men proposing and then with the women proposing gives two different sets
of marriages. Show that your answers illustrate the optimality/pessimality of the algorithm.
- 14B3. Run the Gale-Shapley algorithm with the following sets of preferences with the women proposing:
| Women's Preferences |
| April | Bettie | Carol | Delphi | Eve |
| 1st Choice | F | F | G | G | H |
| 2nd Choice | G | H | I | H | F |
| 3rd Choice | I | I | F | J | I |
| 4th Choice | J | G | H | I | G |
| 5th Choice | H | J | J | F | J |
| Men's Preferences |
| Freddie | Greg | Harold | Isaac | Joe |
| 1st Choice | C | E | A | E | B |
| 2nd Choice | B | B | D | C | D |
| 3rd Choice | E | C | B | A | A |
| 4th Choice | A | A | E | B | C |
| 5th Choice | D | D | C | D | E |
Homework 14A
May 1, 2006
- Ask a question about the previous weeks on a Blackboard
discussion board.
- Complete the
following problems.
- 14A1. 7.2.3
- 14A2. If the missing edge cost in Figure 7.1.4 is 1, find the shortest path from vertex d
to every other vertex in the graph using Dijkstra's Algorithm.
- 14A3. Show that any graph with 2n vertices and smallest degree greater than or equal to
n has a perfect matching.
- 14A4. Give an example of a d-regular graph that does not have a perfect matching for d
greater than or equal to three.
- 14A5. How many perfect matchings does the ladder graph Ln with 2n vertices
contain? (You should give a formula and prove it!)

Homework 13B
April 27, 2006
- Read Section 7.2 and complete the following problems.
- 7.2.1, 7.2.2, (5.1.2 and 5.1.3), 5.1.12
- 13B1. Find the size of a maximum matching in the cycle Cn and the wheel
Wn.
- 13B2. Let G be a bipartite graph that is d-regular. Show that G contains
a perfect matching.
- 13B3. Let G be a bipartite graph that is d-regular. Show that the edges of
G can be decomposed into d disjoint perfect matchings.
Homework 13A
April 24, 2006
- Complete the following problems.
- 13A1. 7.1.10. Explain why your labelings work.
- 13A2. Show that Prim's algorithm also gives the minimum weight spanning tree. Prim's algorithm:
Step 1. Let v be any vertex. Initialize your vertex set S={v} and tree T={v}. Step
2. Find the cheapest edge out of S. Add this edge to your tree T. Step 3. If T is a
spanning tree, stop. Otherwise, repeat Step 2.
- 13A3. Find the minimum cost Traveling Salesman tour of the weighted graph from Figure 7.1.7. Justify
that your answer is correct.
- 13A4. You wish to leave from New York City on a cross-country tour, returning to New York after
visiting once each the following cities:
Boston,
Chicago,
Detroit,
Denver,
Houston,
Los Angeles,
Miami,
Minneapolis,
St Louis,
San Francisco,
Seattle,
and Washington DC.
Use the approximation algorithm from class to find a Hamiltonian cycle through these fourteen cities. You may
find this website useful.
- 13A5. Here is a map of the Western United States with distances
and estimated driving times between cities. Suppose you want to drive from San Francisco to Denver. What is the
best route to take? (Make sure your answer includes a discussion of what `best' means to you.)
Homework 12B
April 20, 2006
- Read Section 7.1 and complete the following problems.
- 7.1.2, 7.1.5, 7.1.8, 7.1.9
- 12B1. Prove that if all the edge costs are different, then there is only one minimum spanning tree.
- 12B2. Find the minimum cost Traveling Salesman tour that visits each vertex in a 3x3 grid.
Justify your answer. (Find a tour that visits each vertex once and returns to the start using as little distance
as possible.)
- 12B3. Find the minimum cost Traveling Salesman tour that visits each vertex in a 4x4 grid.
Homework 10S
Special Practice Homework
- Exam 2: Thursday, April 6, 2006
- Extra Office Hours: Wednesday, April 5, 1:45-3:45
- In preparation for the exam, I have compiled some practice problems.
- 3.2.8, 8.1.4, 8.2.3, 8.2.5, 8.3.2, 8.3.7, 9.1.4, 9.1.5, 9.1.10
- 10S1. For each of the graphs in your table of statistics, find the connectivity, edge connectivity,
independence number, a maximal independent set, a minimal vertex cover and its size, crossing number.
- 10S2. Find a graph that has the following matrix as its adjacency matrix.
| 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 |
- 10S3. How are the adjacency matrices for a graph and its complement related?
- 10S4. Show that in a planar graph G that has girth 5, the number of vertices p and
number of edges q satisfy q <= 5p-10.
- You should also go over your past homework problems.
- Practice making the graphs planar.
Homework 10A
April 3, 2006
- Ask a question about Week 9 on a Blackboard
discussion board.
- Complete the following problems.
- 10A1. Let G be a directed graph with a directed cycle. What can you say about the
entries of the infinite matrix sum I+A1+A2+A3+A4+...? Is this
sum equal to (I-A)-1 in this case? Why or why not?
- 10A2. Draw the binary de Bruijn graph of order n=5. Find one binary de Bruijn sequence of
order 5. (Note: This will be a sequence of length 32.)
- 10A3. Draw the de Bruijn graph of order 3 on the alphabet {0,1,2}. Find one de Bruijn sequence
of order 3 on {0,1,2}.
- 10A4. Prove that there is no closed knight's tour on the 4x4 grid without citing the theorem
from class.
- 10A5. Find a closed knight's tour for the 5x6 grid.
Homework 9B
March 30, 2006
- Read this webpage for an application of
powers of the adjacency matrix (note that the author calls it incorrectly the incidence matrix)
and complete the following problems.
- 9B1. Give an interpretation for the existance of lambda=1 and lambda=-1 as
eigenvalues for a directed cycle, as in Problem 9A4. Besides from lambda=+/-1, what other eigenvalues does
the directed cycle have?
- 9B2. What simple values would you expect for the
eigenvalues of an undirected cycle?
- 9B3. Calculate the number of paths of length 7 from the upper left corner to the right vertex in the
graph from Problem 9A5.
- 9B4. Let G be the star St6 plus an edge. That is, let G be
the graph on seven vertices with degree sequence (6,2,2,1,1,1,1). (a) Use the Matrix Tree Theorem
to find the number of spanning trees of G. (b) Verify your answer by counting the number of
spanning trees by hand.
- 9B5. The other problems we didn't do last Thursday (9.2.4, 8B1, 8B2)
- The open problem on lattices can be found on page 11 of this link. The title of the question is called
``A conjecture on lattice tiles''.
Homework 9A
March 27, 2006
- Ask a question about Week 8 on a Blackboard
discussion board.
- Complete the following problems.
- 9A1. (a) 9.1.11 (b) 9.1.6
- 9A2. 10.3.10
- 9A3. (a) Prove that there is no self-complementary graph on 6 vertices. (b) Find a
self-complementary graph on 5 vertices that is NOT C5.
- 9A4. (a) Find the adjacency matrix A and characteristic polynomial of a directed cycle
Cn=v1->v2->...->vn->v1. (b) For which values
of n is lambda=1 an eigenvalue of A? What about lambda=-1?
Give an eigenvector of A that corresponds to each of these eigenvalues.
- 9A5. Find the incidence and adjacency matrices for the graph pictured below.

Homework 8B
March 23, 2006
- Read Sections 9.2 (to p193) and 10.3 (to p230), and complete the following problems.
- 9.1.7, 9.1.9, 9.2.2, 9.2.4
- 8B1. Try to prove the 4 Color Theorem by emulating the argument from class using Kempe Chains. What
goes wrong?
- 8B2. Show that the contraction of any edge in a tree yields a tree.
- 8B3. (a) Find an embedding of K6 on the torus.
(b) Show that the generalization of Euler's formula holds in this case. (That p-q+r=2-2g.)
Homework 8A
March 20, 2006
- Ask a question about Week 7 on a Blackboard
discussion board.
- Read Sections 8.2 (pp156-157 top, Lemma 8.2.2, pp161-163), 8.3, 9.1 (to p184) and complete the
following problems.
- 8A1. 8.1.9
- 8A2. 8.1.14
- 8A3. 8.2.4
- 8A4. 8.4.11
- 8A5. 9.1.1
Homework 7B
March 9, 2006
- Read Section 8.1 and complete the following problems.
- 8.1.2, 8.1.5, 8.1.7, 8.1.15
- 7B1. Let G be a 2-connected graph with at least three vertices. Prove that there are two
adjacent vertices v and w such that G \ v \ w is still connected. [Hint:
Consider a spanning tree.]
- 7B2. Find the planar dual of the wheel Wn.
Homework 7A
March 6, 2006
- Ask a question about Week 6 on a Blackboard discussion board.
- Complete the following problems.
- 7A1. Determine the independence number and exhibit an independent set of that size for each of the
following graphs: Tetrahedron, Cube, Octahedron, Icosahedron, Dodecahedron. [You should explain why there is no
larger independent set.]
- 7A2. Show that the Petersen graph P is 3-connected, and determine its edge connectivity.
- 7A3. For some k greater than or equal to 2, find a k-regular graph that has a bridge.
- 7A4. (a) Prove or disprove: Every 3-connected graph has no bridge.
(b) Prove or disprove: Every 3-edge-connected graph has no cut vertex.
- 7A5. Prove that the block graph of any connected graph is a tree. [Hint: What two things do you have to prove?]
Homework 6B
March 2, 2006
- Read Section 4.3 and complete the following problems.
- 4.3.2, 4.3.3
- 6B1. Six random points in space are joined pairwise by 15 line segments, where all the
segments are of different length. Prove that at least one of the 15 segments serves as the shortest side
in one of the triangles it is in, and as the longest side in another. [Hint: Use Ramsey Theory.]
- 6B2. Suppose that P and Q are two paths of maximum length in a connected graph
G. Prove that P and Q share a common vertex. [Yes, same as 5S1.]
- 6B3. Show that the wheel graph Wn is 3-connected for all n.
- 6B4. Find a cut set and a separating set for each of the following graphs. What is the
connectivity and edge connectivity for each graph?

Homework 5S
Special Practice Homework
- Exam 1: Thursday, February 23, 2006
- Extra Office Hours: Wednesday, February 22, 1:45-3:45
- In preparation for the exam, I have compiled some practice problems.
- 2.3.2, 2.4.5, 2.4.7, 2.4.8, 3.1.1, 3.1.7, 3.1.9
- 5S1. Suppose that P and Q are two paths of maximum length in a connected graph G.
Prove that P and Q share a common vertex.
- 5S2. Suppose T and T' are two spanning trees of the connected graph G, and let
e is an edge in E(T)\E(T'). Prove that there exists an edge e' in
E(T)\E(T') such that T'+e-e' and T+e'-e are spanning trees of G
- 5S3. Prove that no 3-regular graph (cubic graph) has a decomposition into copies of
P5.
- 5S4. (a) Find a graph E which has an Eulerian circuit but no Hamilton cycle.
(b) Find a graph H which has a Hamilton cycle but no Eulerian circuit.
- You should also go over your past homework problems.
Homework 5A
February 20, 2006
- Ask a question about Week 4 on a Blackboard discussion board.
- Read Section 2.3 and complete the following problems.
- 5A1. Is Figure 2.1.5 critical? Justify.
(Don't believe everything you read!)
- 5A2. Emulate the proof of Theorem 2.1.3 when the chromatic number of a graph is 5.
- 5A3. (a) 2.2.1 [Use logic.]
(b) 2.2.2 [One picture and about one sentence should suffice.]
- 5A4. Show that no perfect matching exists in both halves of Figure 2.2.6
- 5A5. 2.3.11
- Bonus: Give a correct solution to Exercise 2.1.3.
Homework 4B
February 16, 2006
- Read Section 2.2 and complete the following problems.
- 4B1. Describe the most general 2-regular graph. Prove that all 2-regular graphs fit your
description.
- 2.1.15, 2.1.24, 2.2.5, 2.2.9, 2.3.1
Homework 4A
February 13, 2006
- Ask
a question about Week 3 on a Blackboard discussion board.
This week: A bonus homework
point for a question
related to class in the past three weeks, and an additional bonus point for replying to someone else's
post.
- Read Section 2.1 and complete the following problems.
- 2.1.7
- 2.1.11 (Justify your answer)
- 2.1.16
- 2.1.17
- 4A5. Determine the following statistics for the graph below: |V(G)|, |E(G)|, clique number, chromatic
number, girth, diameter, largest degree, smallest degree. Explain your answers for clique number, chromatic
number, girth, and diameter.
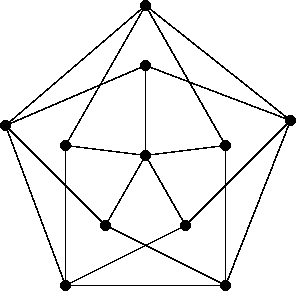
Homework 3B
February 9, 2006
- Read Section 2.1 and complete the following problems.
- 2.1.3, 2.1.4, 2.1.12, 2.1.13
- In the dictionary of graphs, including
-
Path (Pn),
Cycle (Cn),
Wheel (Wn),
Star (Stn),
Complete (Kn),
Complete bipartite (Km,n),
n-dimensional Cube graph (Qn), and the
Petersen graph,
- create a table of the following statistics for each entry:
- |V(G)|, |E(G)|, clique number, chromatic number, girth, diameter,
largest degree, smallest degree
Homework 3A
February 6, 2006
- Ask a question about Week 2 on Blackboard.
- Complete the following problems.
- 1.3.12
- 3A2. Let G be a graph that has a cycle C, and let e be some edge in the cycle.
Remove e
from G to create a graph H. Show that if
there is a path from vertex v to vertex w in G, there is also a path between these same
vertices in H. [Note: There are no restrictions on G. G may have more than the one cycle; it may
even be disconnected.]
- 3A3. Explore the proof of Theorem 1.1.2: The graph below has degree sequence
(S1) 4 4 3 3 3 2 2 2 2 1.
Define (S2) to be 3 2 2 2 2 2 2 2 1.
Walk through the steps of the proof of Theorem 1.1.2 in the following way.
- Determine the vertex S (vertex v* from class), the vertices Ti (or
vi from class), and the vertices Di (or wi from class)
- If you delete vertex S, does the new graph have degree sequence
(S2)?
- Use the method in the proof to modify the graph to be such that removing S gives a graph with
degree sequence (S2).
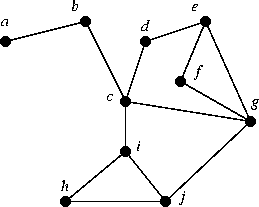
- 3A4. In class on Wednesday, we calculated the number of unlabeled trees and labeled trees on 4
vertices.
Calculate the number of unlabeled trees and labeled trees on 5 vertices, and verify that Cayley's Theorem
holds for n=5.
- 3A5. We know that in a tree with n vertices, the number of edges is n-1. Prove or
disprove: Any graph with n vertices that has fewer than n-1 edges is a forest.
Homework 2B
February 2, 2006
- Read Section 1.3 and complete the following problems.
- 1.2.8
- 1.3.1
- 1.3.2
- 1.3.11
- 1.3.13
- 1.3.14
Homework 2A
January 30, 2006
- Ask a question about Week 1 on the Web Quiz on Blackboard.
- Read Section 1.2 and complete the following problems.
- 1.1.4
- 1.1.5
- 1.1.6
- 1.2.4
- Prove that at a party with 49 people, there is always a person who knows an even number of
others. [Assume acquaintence is mutual.]
Homework 1B
January 26, 2006
- Thoroughly read the class web page including the syllabus and schedule. This should answer all the questions
that you may have about the class.
- Go to the class Discussion Board. Introduce yourself on the "Class Introductions" thread.
- Read Section 1.1 and complete the following problems.
- 1.1.1
- 1.1.2ab, both without using theorem 1.1.2
- 1.1.9ab
- 1.1.10
Back to the Math 381 Home Page.
To Chris's Math Home Page.
Binghamton University
Department of Mathematical Sciences
|




